In Geographic Information Systems, often a region needs to be expanded to include everything within a certain distance, creating a “buffer” zone. For example, you may want to query everything that is within a mile of a shoreline or in the wider corridor of a highway. This operation is also useful in photo editing, computer vision, and robot motion planning.
If the region is stored in a square quadtree, Ang et al. showed that these regions can be quickly approximated using the L∞-norm (i.e. the chessboard distance) instead of euclidean distance.
Sometimes, though, maps are stored in triangular quadtrees, for example in astronomy applications. For these cases, the chessboard distance cannot be used, and the algorithm of Ang et al. is not directly applicable.
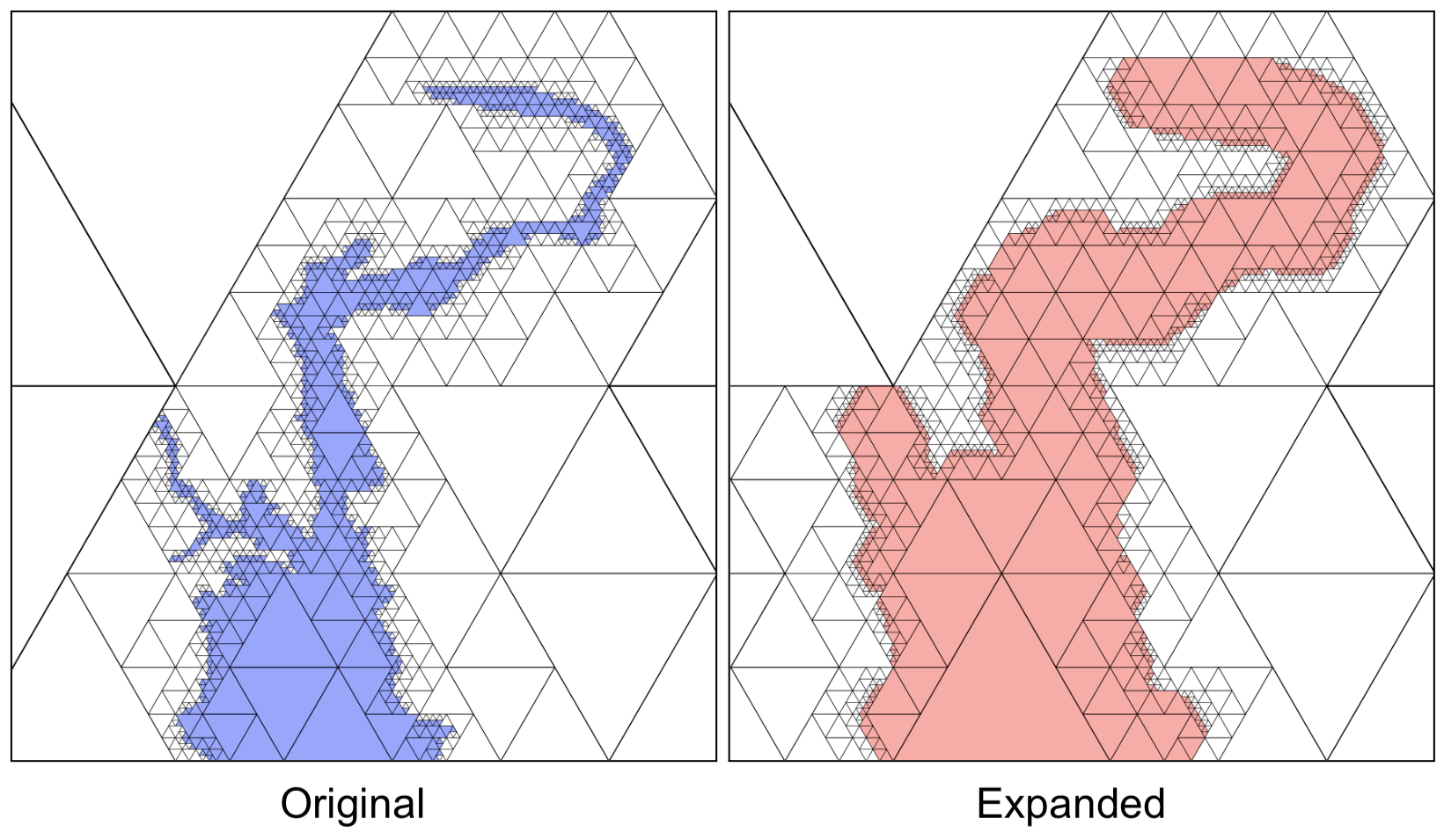
Using the principles of the original method by Ang et al., we create a new algorithm that quickly approximates region expansion in triangular quadtrees, using a triangle-friendly, hexagonal norm instead of the L∞-norm. We show that this algorithm can perform similarly to the square quadtree case, greatly accelerating the operation versus a naïve method.